【どちらが有利!?】単利と複利について解説

こんにちは!
アラサー係長です!
前回の記事では利回りについて勉強しました!
投資による運用には「利回り」が大きいほど有利ということを学びましたね。
今回は、その「利回り」について更に深堀し知っておきたい知識になります。
それが「単利」と「複利」についてです。

たまーに聞いたことあるワードだけど違いはなんだろう…。
一緒に勉強していきましょう!
単利とは?
まず、単利について簡単に見ていきましょう!
「単利」:預けた元本のみに利息がつくこと
単利は預けた金額(元本)対してのみ利息がつく金利のことです。

言葉だけだと分かりづらいので、例を挙げ詳しく見ていきましょう。
例えば、100万円預けて年利が10%の場合、1年間の利息は10万円です。
2年目も元本100万円を元に計算するため、2年目も10万円の利息を得たことになります。
そうすると、2年間で増えた金額はトータル20万円ということになります。
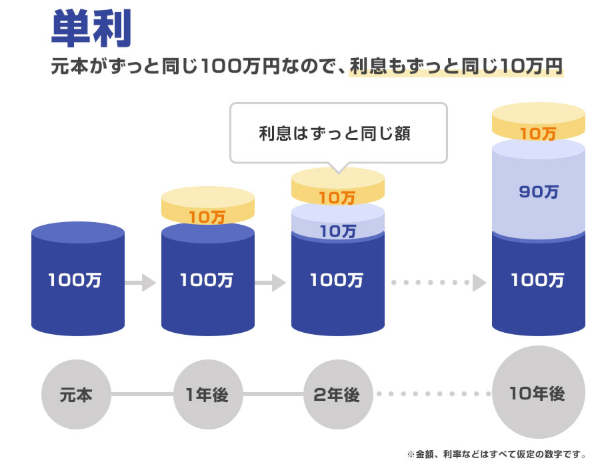
単利の場合、計算はシンプルですよね。
複利とは?
一方、複利とは以下の通りになります。
「複利」:元本+利息分 に利息がつく
要するに、元本に利息が付いたものを、新元本として利息を計算していくことになります。

ん? ちょ、ちょっと例をください!
例えば100万円預けて年利が10%の場合、年間の利息は10万円です。
ここまでは単利と同じです。
しかし、2年目からは元本が「100万円+利息分10万円」となり「110万円」となります。
2年目はこの 110万円 に年利10%をかけることになるため、増えた金額は
トータル21万円となります。
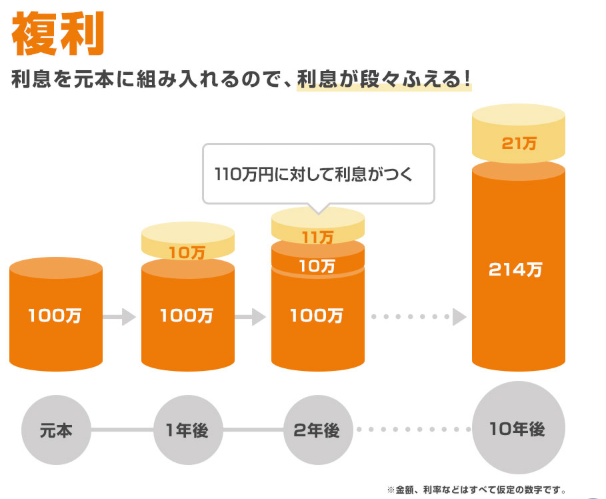
単利と比べて、2年目で差があることが分かります。
元本がその都度増えるため、長期的にみると利息分もどんどん拡大します
これを「複利の力」と呼びます。
「複利の力」とは?
20世紀最大の物理学者とも言われるアインシュタインが「宇宙で最も偉大な力」と呼んだのがこの「複利の力」になります。

アルベルト・アインシュタイン(1879年3月14日 - 1955年4月18日)は、ドイツ生まれの理論物理学者である。
特殊相対性理論および一般相対性理論、相対性宇宙論などを提唱した業績で知られる。それまでの物理学の認識を根本から変え、「20世紀最高の物理学者」とも評される。光量子仮説に基づく光電効果の理論的解明によって1921年のノーベル物理学賞を受賞。
出典: フリー百科事典『ウィキペディア(Wikipedia)』
複利の力を示すエピソード
歴史をさかのぼると「複利の力」を象徴した逸話が数多く存在します。
戦国時代の話ですが、豊臣秀吉が、ある一人と将棋をしていた際のエピソードです。
その人物は、秀吉に勝利し褒美を貰うことになりました。
その時にこう述べたようです。
「まず、将棋のマス目に米を1粒ください」
秀吉は、欲が無い人物だな…。と感心しながら要望に応えます。
「次のマス目に倍の2粒。次のマス目に4粒」とマス目ごとに倍にしていく要望をしました。
最終的には、これを繰り返してマス目が一杯になるまでお願いされた秀吉ですが、
途中で蔵の米が全て無くなってしまうことに気が付き、慌てて取り消したというお話です。
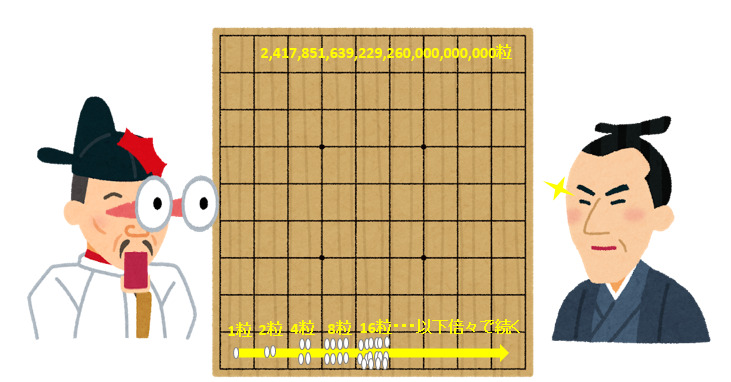
もし全てのマス目を埋めることになると、「2,417,851,639,229,260,000,000,000粒」にもなります。

数えられないですよね!!!
ちなみに、これが「単利」の場合、マス目と同じ数の「81粒」です。
この時代からも「複利の力」は偉大なものであったことがよく分かります。
単利と複利の運用比較
同じ100万円を30年間10%で運用した場合、単利と複利ではこのような差が生まれます。
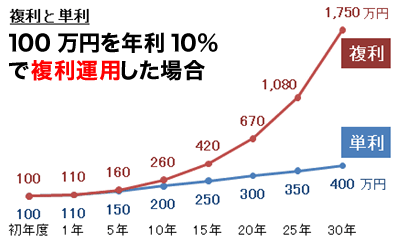
運用年数が長ければ長いほど、単利と複利の差は大きくなることが分かります。
複利運用では、20年で約2倍、30年では4倍以上もリターンが大きくなります!
投資の世界で「早く投資を始めた方が有利」といわれるのは、
この複利の力を長期的に活かすことに繋がるためです。

複利の力すごいですね!!!
電卓で複利計算してみよう
複利の力が理解できて来たところで、実際に計算をしてみましょう。
電卓で簡単に計算できます。
電卓編
例)元本100万円を 年利5% で5年間運用した場合の増加額は?
●ステップ1(1年目:単利計算)
1 + 0.05 × = と電卓を押します
すると、 1.05 と表示されたかと思います。
●ステップ2(2年目:複利計算)
次に、= を押してみてください。
すると、 1.1025 と表示されたと思います。
●ステップ3(3~5年目:複利計算)
そのまま = を押していきます
3年目:1.157625
4年目:1.21550625
5年目:1.2762815625 と変化すると思います。
●ステップ4(増加額計算)
5年目の 1.2762815625 に元本の100万円をかけましょう
すると、1,276,281.5625円と表示されます。
100万円が5年間で約28万円増えたことになります。
ちなみに単利ですと、単利1年目の増加額+5万円×年数5年で計算できトータル25万円増えたということになります。
このように電卓でも簡単に複利を計算できます。
但し、運用期間が30年などの長期になると電卓計算も面倒ですので計算シュミレーションサイトなどを使うのがおすすめです。
計算シュミレーションサイト
単純な複利の計算はCASIOが提供している- 高精度計算サイト - Keisan -を使用してます。
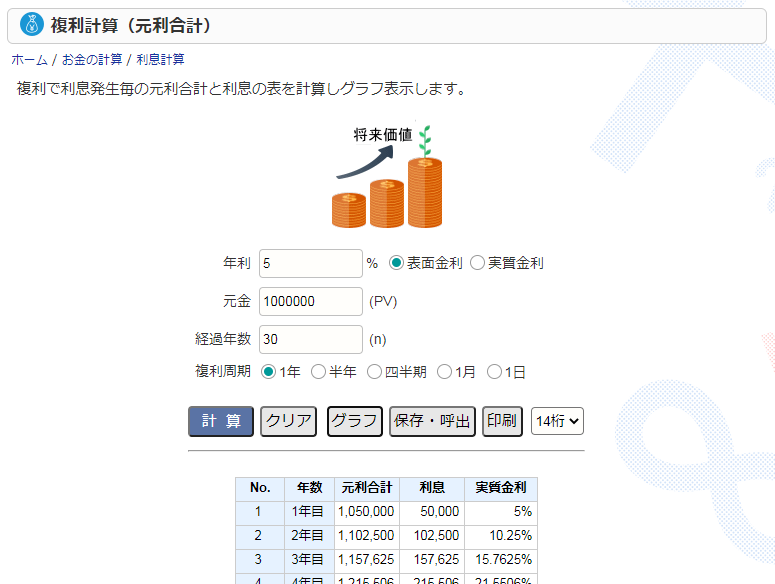
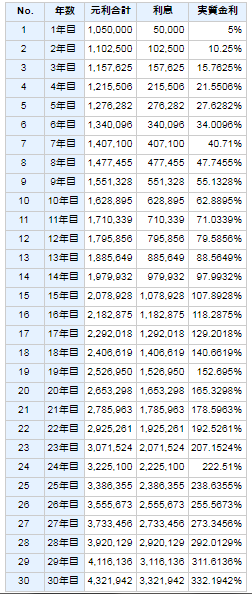
上記の表が簡単に表示され、長期間での複利がどのように増加するか確認できます。
また、積立などの長期間運用も複利の力が働きます。
その際に元本がいくら増えるのか? リターンを確認する必要があります。
私は、楽天証券の「積立かんたんシミュレーション」を使用してます。

条件に合わせて入力するとグラフが出てきますので分かりやすいです。
実際に自分で様々な数字を入力してみると面白いと思います!
期間や積立額、リターン率を変えることで
え? こんなに増えるの? と感じるかもしれません。
まとめ
いかがでしたか?
今回は「単利」と「複利」について勉強しました。
義務教育で教えてくれよー。と感じる内容でしたよね
投資を行う際は、是非とも「複利の力」の恩恵を受けたいものです!
今回は以上となります。
最後までご覧いただきありがとうございました!
では、また!